図形の描画1
点の描画
文字も画像も、画面に表示されるものはすべて点の集まりです。
この点をピクセルといいます。
これは画像などが持つ色情報の最小単位で、様々な色のピクセルが集まることで絵や文字を表現しています。
まずはピクセルを画面に描画してみましょう。
SetPixel関数
点や図形など描画もデバイスコンテキストを通して行います。
画面の任意の位置にピクセルを描画するにはSetPixel関数を使用します。
- COLORREF SetPixel(
HDC hdc,
int x,
int y,
COLORREF color
); - 座標(x, y)にcolor色の点を描画する。
戻り値は実際に描画された色。
失敗した場合は-1を返す。
説明の通りで、特に難しくはない関数です。
COLORREF型に関しては文字色と背景色を参照してください。
GetPixel関数
対になる関数なのでついでに紹介します。
GetPixel関数は、指定の座標のピクセルの色を取得します。
- COLORREF GetPixel(
HDC hdc,
int x,
int y
); - 座標(x, y)の色情報を取得する。
説明の通りです。
線の描画
MoveToEx関数、LineTo関数
理屈上はどんな図形でもSetPixel関数で描画できますが、本当にこれだけでやろうとすると大変なのでほかにも関数が用意されています。
線を描画するにはMoveToEx関数とLineTo関数を使用します。
- BOOL MoveToEx(
HDC hdc,
int x,
int y,
LPPOINT lppt
); - 現在の座標を(x, y)にセットし、以前の座標をlpptに格納する。
成功した場合は0以外を、失敗した場合は0を返す。
- BOOL LineTo(
HDC hdc,
int x,
int y
); - 現在位置から座標(x, y)まで直線を描画する。
現在位置は座標(x, y)に更新される。
成功した場合は0以外を、失敗した場合は0を返す。
線は「座標Aから座標Bまでの直線を描画する」という手順で行います。
そのためには、まず起点となる「現在の座標」をMoveToEx関数で設定します。
引数のlpptにはMoveToEx関数を実行する直前の現在位置が格納されますが、必要なければNULLを指定することもできます。
線の終端座標はLineTo関数で指定します。
LineTo関数は指定の座標の直前までを描画します。
(指定座標のピクセルには描画されません)
描画後、現在位置は指定の座標に更新されます。
サンプルコード
ここまでのサンプルコードです。
//ウィンドウプロシージャ
LRESULT CALLBACK WndProc(HWND hWnd, UINT message, WPARAM wParam, LPARAM lParam)
{
HDC hdc;
PAINTSTRUCT ps;
switch (message)
{
case WM_PAINT: //ウィンドウの描画
hdc = BeginPaint(hWnd, &ps);
for (int i = 0; i < 256; i++) {
SetPixel(hdc, i + 10, 10, RGB(i, 255 - i, 0));
}
MoveToEx(hdc, 10, 20, NULL);
LineTo(hdc, 110, 20);
LineTo(hdc, 110, 70);
LineTo(hdc, 210, 70);
EndPaint(hWnd, &ps);
break;
case WM_DESTROY: //ウィンドウの破棄
PostQuitMessage(0);
break;
default:
return DefWindowProc(hWnd, message, wParam, lParam);
}
return 0;
}
最初にSetPixel関数で色を少しずつ変えながら直線を引いています。
次にLineTo関数でより手軽に線を引いています。
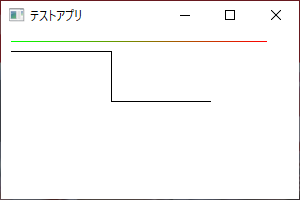
LineTo関数で色を変える方法は別の機会に説明します。
連続した直線の描画
PolylineTo関数、Polyline関数
線はLineTo関数を使えば描けますが、折れ線グラフのような連続した直線はPolylineTo関数やPolyline関数を使用したほうがコードが簡単になります。
これらの関数は座標情報を表すPOINT構造体の配列を使用します。
- BOOL PolylineTo(
HDC hdc,
const POINT *apt,
DWORD cpt
); - 現在位置から座標の配列aptの要素を順に直線でcpt本描画する。
成功した場合は0以外を、失敗した場合は0を返す。
- BOOL Polyline(
HDC hdc,
const POINT *apt,
int cpt
); - 座標の配列aptの要素を順に直線でcpt本描画する。
成功した場合は0以外を、失敗した場合は0を返す。
- typedef struct tagPOINT {
LONG x;
LONG y;
} POINT, *PPOINT; - 座標情報を格納する構造体。
第二引数aptはPOINT構造体の配列を指定します。
第三引数cptは第二引数の配列の要素数を指定します。
両者の違いは「現在の座標」を使用するかしないかです。
現在の座標を使用しないPolyline関数では必ず2つ以上の座標情報が必要になります。
(配列の先頭要素の座標が起点となる)
//ウィンドウプロシージャ
LRESULT CALLBACK WndProc(HWND hWnd, UINT message, WPARAM wParam, LPARAM lParam)
{
HDC hdc;
PAINTSTRUCT ps;
POINT points[5] = {
{10, 10},
{80, 10},
{10, 110},
{80, 110},
{10, 10}
};
switch (message)
{
case WM_PAINT: //ウィンドウの描画
hdc = BeginPaint(hWnd, &ps);
PolylineTo(hdc, points, 5);
//Polyline(hdc, points, 5);
EndPaint(hWnd, &ps);
break;
case WM_DESTROY: //ウィンドウの破棄
PostQuitMessage(0);
break;
default:
return DefWindowProc(hWnd, message, wParam, lParam);
}
return 0;
}
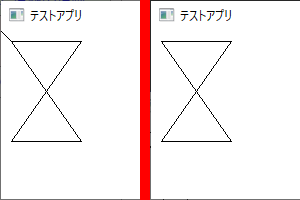
左がPolylineTo関数、右がPolyline関数の実行結果です。
PolylineTo関数は現在位置を起点とするため、初期値である(0, 0)の位置から描画が開始されています。
Polyline関数は配列の先頭要素を起点とするので、(10, 10)の位置から描画が開始されます。
PolyPolyline関数
連続した直線を複数個描画するPolyPolylineという関数もあります。
- BOOL PolyPolyline(
HDC hdc,
const POINT *apt,
const DWORD *asz,
DWORD csz
); - 連続した直線を複数個描画する。
第二引数aptはPOINT構造体の配列です。
第三引数aszはDWORD型(unsigned long型)の配列で、この配列の要素数が「連続した直線」の数になります。
配列の各要素には「連続した直線」が持つ頂点の数を指定します。
そのため、各要素は必ず2以上の値が必要です。
また、各要素を合計した値は配列aptの要素数以下にする必要があります。
第四引数cszは配列aszの要素数の指定です。
実際に描画する「連続した直線」の数の指定となります。
//ウィンドウプロシージャ
LRESULT CALLBACK WndProc(HWND hWnd, UINT message, WPARAM wParam, LPARAM lParam)
{
HDC hdc;
PAINTSTRUCT ps;
POINT points[] = {
{10, 10},
{60, 110},
{110, 10},
{160, 110},
{210, 10},
{10, 60},
{210, 60}
};
DWORD vertices[] = {
5, 2
};
switch (message)
{
case WM_PAINT: //ウィンドウの描画
hdc = BeginPaint(hWnd, &ps);
PolyPolyline(hdc, points, vertices, 2);
EndPaint(hWnd, &ps);
break;
case WM_DESTROY: //ウィンドウの破棄
PostQuitMessage(0);
break;
default:
return DefWindowProc(hWnd, message, wParam, lParam);
}
return 0;
}
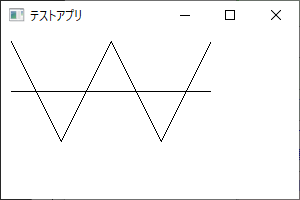
「W」型の図形と、それを横に貫く直線を描画しています。