ビット演算
ビットとは
コンピューターの内部ではすべてのデータを0と1の二種類だけで扱っています。
これを二進数といいます。
C#ではint型やstring型などの様々なデータ型が用意されていますが、これらも内部的にはすべて0と1の羅列です。
コンピューターで扱うデータの最小単位はビットといいます。
これは「1」か「0」か、つまり「ある」か「ない」かの2通りだけを表せる単位です。
電気的に「オン」か「オフ」かの状態の判定だけで良いのでコンピューターにとって二進数は都合が良いのです。
1ビットで2通りを表せるので、2ビットでは「2通り×2通り」で4通りの情報を扱うことができます。
(2の2乗)
3ビットならば「2通り×2通り×2通り」で8通りです。
(2の3乗)
つまり1ビット増えるごとに扱える情報量が倍になります。
C#で扱える最小のデータ型は「byte型」「sbyte型」「bool型」で、それぞれ1バイトです。
1バイトはビットに換算すれば8ビットのサイズとなります。
つまりbyte型は「0~255」、sbyte型は「-128~127」とそれぞれ256通り(2の8乗)の数値を扱うことができます。
(データ型参照)
bool型は「true」か「false」かの二通りだけなので1ビットで足りるのですが、内部的には1バイトのサイズとなっています。
これはおそらく処理効率の都合と思われます。
(残りの7ビットを無駄にしてでも、1バイト単位で扱った方が効率が良い)
二進数での表記(符号なし)
以下に、符号なしのデータ型の各数値を二進数で表したときのビットの並びを示します。
byte[] bytesA = new byte[]
{
1, 2, 3, 4, 5, 6, 7, 8
};
byte[] bytesB = new byte[]
{
248, 249, 250, 251, 252, 253, 254, 255
};
foreach (var b in bytesA)
{
Console.Write(Convert.ToString(b, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", b);
}
Console.WriteLine("...");
foreach (var b in bytesB)
{
Console.Write(Convert.ToString(b, 2).PadLeft(8, '0'));
Console.WriteLine(" ({0})", b);
}
00000001(1) 00000010(2) 00000011(3) 00000100(4) 00000101(5) 00000110(6) 00000111(7) 00001000(8) ... 11111000 (248) 11111001 (249) 11111010 (250) 11111011 (251) 11111100 (252) 11111101 (253) 11111110 (254) 11111111 (255)
Convert.ToStringメソッドは引数に指定した数値を文字列に変換するメソッドです。
第二引数に「2」を指定すると二進数に変換されます。
PadLeftメソッドは指定の桁数になるまで文字列の左側に任意の文字で埋めるメソッドです。
詳しくは文字列の操作 - PadLeft、PadRight参照。
上記以外の範囲は以下のツールで確認できます。
二進数での表記(符号あり)
負数(0未満の数)を扱えるデータ型の場合は、最上位ビット(一番左端の桁)が0の場合はプラス値を、1の場合はマイナス値を表します。
sbyte[] sbytesA = new sbyte[]
{
1, 2, 3, 4
};
sbyte[] sbytesB = new sbyte[]
{
124, 125, 126, 127
};
sbyte[] sbytesC = new sbyte[]
{
-1, -2, -3, -4
};
sbyte[] sbytesD = new sbyte[]
{
-125, -126, -127, -128
};
foreach (var b in sbytesA)
{
Console.Write(Convert.ToString((byte)b, 2).PadLeft(8, '0'));
Console.WriteLine(" ({0})", b);
}
Console.WriteLine("...");
foreach (var b in sbytesB)
{
Console.Write(Convert.ToString((byte)b, 2).PadLeft(8, '0'));
Console.WriteLine(" ({0})", b);
}
Console.WriteLine("...");
foreach (var b in sbytesC)
{
Console.Write(Convert.ToString((byte)b, 2).PadLeft(8, '0'));
Console.WriteLine(" ({0})", b);
}
Console.WriteLine("...");
foreach (var b in sbytesD)
{
Console.Write(Convert.ToString((byte)b, 2).PadLeft(8, '0'));
Console.WriteLine(" ({0})", b);
}
00000001 (1) 00000010 (2) 00000011 (3) 00000100 (4) ... 01111100 (124) 01111101 (125) 01111110 (126) 01111111 (127) ... 11111111 (-1) 11111110 (-2) 11111101 (-3) 11111100 (-4) ... 10000011 (-125) 10000010 (-126) 10000001 (-127) 10000000 (-128)
Convert.ToStringメソッドはsbyte型を二進数で表示するオーバーライドメソッドが存在しないので、byte型にキャストしてからメソッドを実行しています。
符号付き型の場合は最上位ビットはプラスかマイナスかを表すので、sbyte型の最大値である「127(01111111)」の次の値は負数(-128(10000000))になります。
上記以外の範囲は以下のツールで確認できます。
ビット演算
ビット演算は、データを上記のような「0と1」の並びと見立て、各桁を直接操作する演算方法です。
ビット演算には論理演算とシフト演算があります。
論理演算
論理演算は二進数の各桁同士を直接演算します。
論理演算子は以下の四種類があります。
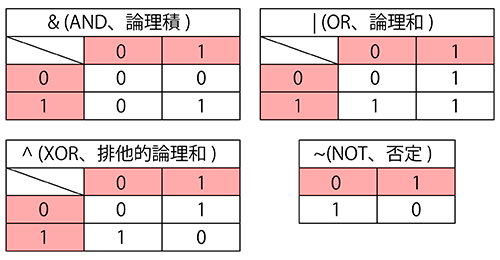
- a & b
AND(論理積) - aとbの両方が1なら1にセット
それ以外は0にセット - a | b
OR(論理和) - aとbの少なくとも一方が1なら1にセット
両方が0なら0にセット - a ^ b
XOR(排他的論理和) - aとbの値が異なるなら1にセット
それ以外は0にセット
- ~a
NOT(否定) - aを反転
AND、OR、XORの三つは複合代入演算子もあります。
- a &= b
- aとbの論理積をaに代入
- a |= b
- aとbの論理和をaに代入
- a ^= b
- aとbの排他的論理和をaに代入
この図だけでは論理演算のイメージが湧きにくいと思うので、それぞれ例を出して説明します。
&(AND、論理積)
&演算子(論理積)は「各桁同士を比較して両方が1ならば1を返す」演算子です。
一方または両方が0ならば0を返します。
例えば、
「5」を二進数になおすと「00000101」となります。
「9」を二進数になおすと「00001001」となります。
(8ビット分のサイズと考えた場合)
二進数のそれぞれの桁を比較すると、両方の桁が「1」になるのは一桁目だけです。
これを論理積で演算すると、「00000001」(二進数で「1」)が返されます。
int num5 = 5;
int num9 = 9;
//論理積
int numCalc = num5 & num9;
Console.Write(Convert.ToString(num5, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", num5);
Console.Write(Convert.ToString(num9, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", num9);
Console.WriteLine("{0} & {1} =", num5, num9);
Console.Write(Convert.ToString(numCalc, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", numCalc);
00000101(5) 00001001(9) 5 & 9 = 00000001(1)
「5」と「9」の演算で「1」になるのは四則計算ではあり得ませんが、ビット演算では四則計算のことは忘れてください。
なお、ビット演算子を使用できるのはint型、uint型、long型、ulong型のいずれかの型となります。
int型(uint型)より小さいデータ型を使用した場合はint型(uint型)に暗黙的に変換されます。
&演算子、|演算子、^演算子はbool型に対しても使用できます。
&&、||はショートサーキットで評価します。
こちらはbool型のみに使用できます。
(^演算子は両方を評価しないと結果がわからないのでショートサーキットはない)
|(OR、論理和)
|演算子(論理和)は「各桁同士を比較して両方または一方が1ならば1を返す」演算子です。
両方が0ならば0を返します。
int num5 = 5;
int num9 = 9;
//論理和
int numCalc = num5 | num9;
Console.Write(Convert.ToString(num5, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", num5);
Console.Write(Convert.ToString(num9, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", num9);
Console.WriteLine("{0} | {1} =", num5, num9);
Console.Write(Convert.ToString(numCalc, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", numCalc);
00000101(5) 00001001(9) 5 | 9 = 00001101(13)
^(XOR、排他的論理和)
^演算子(排他的論理和)は「各桁同士を比較して一方のみが1の場合に1を返す」演算子です。
両方の値が同じ場合は0を返します。
(1同士、または0同士)
つまり両方の値が異なる場合は1、同じ場合は0となります。
int num5 = 5;
int num9 = 9;
//排他的論理和
int numCalc = num5 ^ num9;
Console.Write(Convert.ToString(num5, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", num5);
Console.Write(Convert.ToString(num9, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", num9);
Console.WriteLine("{0} ^ {1} =", num5, num9);
Console.Write(Convert.ToString(numCalc, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", numCalc);
00000101(5) 00001001(9) 5 ^ 9 = 00001100(12)
~(NOT、否定)
~演算子(否定)は「各桁のビットを反転する」演算子です。
これは補数演算子ともいいます。
~演算子は他のビット演算子とは違い、単体(右辺のみ)で使用します。
int num5 = 5;
int num9 = 9;
Console.Write(Convert.ToString((byte)num5, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", num5);
Console.Write(Convert.ToString((byte)~num5, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", ~num5);
Console.WriteLine();
Console.Write(Convert.ToString((byte)num9, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", num9);
Console.Write(Convert.ToString((byte)~num9, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", ~num9);
00000101(5) 11111010(-6) 00001001(9) 11110110(-10)
!(NOT、論理否定)
~演算子はbool型には使用できません。
bool型を反転するには!演算子(論理否定)を使用します。
詳しくは論理否定を参照。
シフト演算
シフト演算は、0と1の並びをごそっと左右に移動(シフト)させてしまう演算方法です。
シフト演算には左シフトと右シフトの二種類があります。
演算子も二種類あります。
- a << b
- aを左にb桁シフトする
- a >> b
- aを右にb桁シフトする
全角文字に「≪」「≫」がそれぞれありますが、それではなく半角の「<」「>」を二つ重ねた演算子です。
また、以下の複合代入演算子もあります
- a <<= b
- aを左にb桁シフトし、aに代入する
- a >>= b
- aを右にb桁シフトし、aに代入する
「0と1の並びを左右にシフトする」というのは以下のようなイメージです。
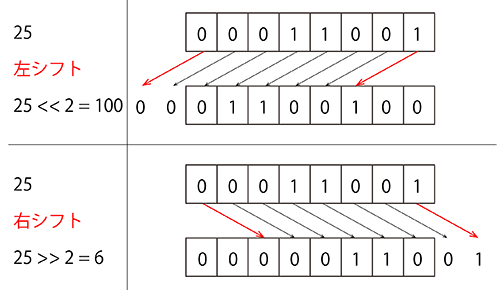
数値を二進数で表し、その桁を右辺の数値でそのまま移動させてしまうのがシフト演算です。
シフトの結果、はみ出した桁は削除されます。
空いた桁に何が入るかは後述します。
シフト演算は「左に1つシフトすると、値が倍になる」という特徴があります。
反対に、「右に1つシフトすると、値が半分になる」という特徴があります。
(小数点以下は切り捨て)
これは十進数の時と考え方は同じです。
例えば十進数の「300」を左に一桁移動すると「3000」となり「10倍」の値となります。
反対に右に一桁移動すると「30」となり、「1/10倍」となります。
十進数の場合は10倍(1/10倍)、二進数の場合は2倍(1/2倍)、というわけです。
論理シフトと算術シフト
シフト演算の方法には論理シフトと算術シフトの二種類があります。
これは、シフトの結果空いた桁に何を入れるかが異なります。
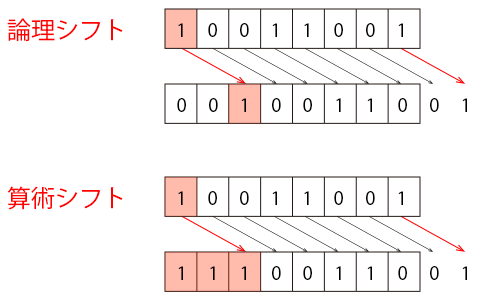
論理シフトは、空いた桁は常に「0」で埋める方法です。
左シフトの場合は数学的に正しくシフト可能です。
右シフトの場合、元の値が負数(マイナス)の場合は正負が逆転することになります。
(最上位ビットが正負を表すため)
算術シフトは、右シフトと左シフトで動作が異なります。
右シフトの場合は空いた桁は元の最上位ビットと同じ値で埋められます。
左シフトの場合は論理シフトと同じく常に「0」で埋められます。
この方法は符号付き整数の場合は正数でも負数でも正しくシフト可能です。
しかし符号なし整数の場合、右シフトは数学的に正しくありません。
C#では、符号付き整数の場合は算術シフトで、符号なし整数の場合は論理シフトで行われます。
つまり左右どちらの場合でも数学的に正しくシフトできます。
byte a = 25;
Console.Write(Convert.ToString(a, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", a);
//左シフト
byte aL = (byte)(a << 1);
Console.Write(Convert.ToString(aL, 2).PadLeft(8, '0'));
Console.WriteLine("({0}, a << 1)", aL);
//右シフト
byte aR = (byte)(a >> 1);
Console.Write(Convert.ToString(aR, 2).PadLeft(8, '0'));
Console.WriteLine("({0}, a >> 1)", aR);
Console.WriteLine();
sbyte b = -25;
Console.Write(Convert.ToString((byte)b, 2).PadLeft(8, '0'));
Console.WriteLine("({0})", b);
//左シフト
sbyte bL = (sbyte)(b << 1);
Console.Write(Convert.ToString((byte)bL, 2).PadLeft(8, '0'));
Console.WriteLine("({0}, b << 1)", bL);
//右シフト
sbyte bR = (sbyte)(b >> 1);
Console.Write(Convert.ToString((byte)bR, 2).PadLeft(8, '0'));
Console.WriteLine("({0}, b >> 1)", bR);
00011001(25) 00110010(50, a << 1) 00001100(12, a >> 1) 11100111(-25) 11001110(-50, b << 1) 11110011(-13, b >> 1)
符号なし右シフト演算子
符号付き型に対する右シフトは、上述の通り算術シフトが使用されます。
C#11以降、符号付き型に対する右シフトを論理シフトで行う>>>演算子が追加されています。
(復号代入は>>>=)
符号なし型に対する右シフトはもともと論理シフトなので、つまりこの演算子は符号の有無に関係なく論理右シフトを行います。
//int型のバイナリ表現を返す
static string BinaryString(int n)
{
string s = Convert.ToString(n, 2).PadLeft(32, '0');
var sb = new System.Text.StringBuilder(s, 39);
for (int i = 28; i > 0; i -= 4)
{
sb.Insert(i, '_');
}
return sb.ToString();
}
static void Main(string[] args)
{
int n = -25;
Console.Write(BinaryString(n));
Console.WriteLine("({0})", n);
//左シフト
int arithmetic = n >> 1;
Console.Write(BinaryString(arithmetic));
Console.WriteLine("({0}, n >> 1)", arithmetic);
//右シフト
int logical = n >>> 1;
Console.Write(BinaryString(logical));
Console.WriteLine("({0}, n >>> 1)", logical);
}
1111_1111_1111_1111_1111_1111_1110_0111(-25) 1111_1111_1111_1111_1111_1111_1111_0011(-13, n >> 1) 0111_1111_1111_1111_1111_1111_1111_0011(2147483635, n >>> 1)